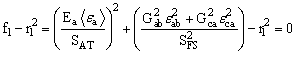User Manual

• Mat162 Home
• User-Manual
• Single Element Studies
• MAT162 Examples
• MAT162 Simulation Movies

• References
• Support

---

Click here for the MAT162-USER-MANUAL-Version-22B-2022.pdf

This model may be used to simulate progressive failure in composite materials consisting of unidirectional and woven fabric layers subjected to high strain-rate and high pressure loading conditions. The model is a generalization of the layer failure model reported in [1]. The MLT damage mechanics approach [2] has been adopted to characterize the softening behavior after damage initiation. This model is available for solid element only (single point integration).

Card Format

Card1	1	2	3	4	5	6	7	8
Variable	MID	RO	EA	EB	EC	PRBA	PRCA	PRCB
Type	I	F	F	F	F	F	F	F
Card2
Variable	GAB	GBC	GCA	AOPT
Type	F	F	F	F
Card3
Variable	XP	YP	ZP	A1	A2	A3
Type	F	F	F	F	F	F
Card4
Variable	V1	V2	V3	D1	D2	D3	BETA
Type	F	F	F	F	F	F	F
Card5
Variable	SAT	SAC	SBT	SBC	SCT	SFC	SFS	SAB
Type	F	F	F	F	F	F	F	F
Card6
Variable	SBC	SCA	SFFC	AMODEL	E_LIMT	PHIC	S_DELM
Type	F	F	F	F	F	F	F
Card7
Variable	OMGMX	ECRSH	EEXPN	CR1	AM1
Type	F	F	F	F	F
Card8
Variable	AM2	AM3	AM4	CR2	CR3	CR4
Type	F	F	F	F	F	F

 

Variable                          Description

MID	Material identification. A unique number has to be chosen.
RO	Mass density
EA	Ea , Young’s modulus – longitudinal direction
EB	Eb , Young’s modulus – transverse direction
EC	Ec , Young’s modulus – through thickness direction
PRBA	nba , Poisson’s ratio ba
PRCA	nca , Poisson’s ratio ca
PRCB	ncb , Poisson’s ratio cb
GAB	Gab , shear modulus ab
GBC	>Gbc , shear modulus bc
GCA	Gca , shear modulus ca
AOPT	Material axes option, see Figure 20.1 in LS-DYNA Manual:EQ. 0.0: locally orthotropic with material axes determined by element nodes as shown in Figure 20.1. Nodes 1, 2, and 4 of an element are identical to the Nodes used for the definition of a coordinate system as by *DEFINE_COORDINATE_NODES.EQ. 1.0: locally orthotropic with material axes determined by a point in space and the global location of the element center, this is the a-direction.EQ. 2.0: globally orthotropic with material axes determined by vectors defined below, as with *DEFINE_COORDINATE_VECTOR.
XP YP ZP	Define coordinates of point p for AOPT = 1.
A1 A2 A3	Define components of vector a for AOPT = 2.
V1 V2 V3	Define components of vector v for AOPT = 3.
D1 D2 D3	Define components of vector d for AOPT = 2.
SAT	Longitudinal tensile strength
SAC	Longitudinal compressive strength
SBT	Transverse tensile strength
SBC	Transverse compressive strength
SCT	Through thickness tensile strength
SFC	Crush strength
SFS	Fiber mode shear strength
SAB	Shear strength, ab plane, see below.
SBC	Shear strength, bc plane, see below.
SCA	Shear strength, ca plane, see below
SFFC	Scale factor for r esidual compressive strength
AMODEL	Material models:EQ. 1: Unidirectional layer modelEQ. 2: Fabric layer model
BETA	Layer in-plane rotational angle in degrees.
PHIC	Coulomb friction angle for matrix and delamination failure
S_DELM	Scale factor for delamination criterion
E_LIMT	Element eroding axial strain
ECRSH	Limit compressive relative volume for element eroding
EEXPN	Limit expansive relative volume for element eroding
OMGMX	Limit damage parameter for elastic modulus reduction
AM1	Coefficient for strain rate softening property for fiber damage in A direction
AM2	Coefficient for strain rate softening property for fiber damage in B direction (For plain weave model only)
AM3	Coefficient for strain rate softening property for fiber crush and punch shear damage
AM4	Coefficient for strain rate softening property for matrix and delamination damage
CR1	Coefficient for strain rate dependent strength properties
CR2	Coefficient for strain rate dependent axial moduli
CR3	Coefficient for strain rate dependent shear moduli
CR4	Coefficient for strain rate dependent transverse moduli

 

MATERIAL MODELS

Failure models based on the 3D strains in a composite layer with improved progressive failure modeling capability are established for a unidirectional or a plain weave fabric composite layer. They can be used to effectively simulate the fiber failure and delamination behavior under high strain-rate and high pressure ballistic impact conditions.

The unidirectional and fabric layer failure criteria and the associated property degradation models are described as follows. All the failure criteria are expressed in terms of stress components based on ply level strains = . The associated elastic moduli are . Note that for the unidirectional model, a, b and c denote the fiber, in-plane transverse and out-of-plane directions, respectively, while for the fabric model, a, b and c denote the in-plane fill, in-plane warp and out-of-plane directions, respectively.

UNIDIRECTIONAL LAMINA DAMAGE FUNCTIONS

The fiber failure criteria of Hashin for a unidirectional layer are generalized to characterize the fiber damage in terms of strain components for a unidirectional layer. Three damage functions are used for fiber failure, one in tension/shear, one in compression, and another one in crush under pressure. They are chosen in terms of quadratic strain forms as follows.

Tension/Shear:
(1)

Compression:
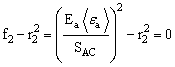(2)

Crush:
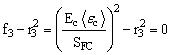(3)

where are Macaulay brackets, SAT and SAC are the tensile and compressive strengths in the fiber direction, and SFSand SFC are the layer strengths associated with the fiber shear and crush failure, respectively. The damage thresholds, r i , i = 1,2,3, have the initial values equal to 1 before the damage initiated, and are updated due to damage accumulation in the associated damage modes.

Matrix mode failures must occur without fiber failure, and hence they will be on planes parallel to fibers. Two matrix damage functions are chosen for the failure plane perpendicular and parallel to the layering planes. They have the forms:

Perpendicular matrix mode:
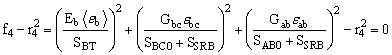(4)

Parallel matrix mode (Delamination):
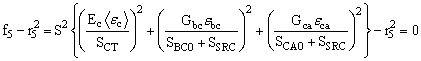(5)

where SBT and SCT are the transverse tensile strengths, and , and are the shear strength values of the corresponding tensile modes ( or ) . Under compressive transverse strain, or , the damaged surface is considered to be “closed”, and the damage strengths are assumed to depend on the compressive normal strains b ased on the Mohr -Coulomb theory, i.e.,
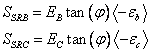(6)

where j is a material constant as tan( j ) is similar to the coefficient of friction. The damage thresholds, r4 and r5 , have the initial values equal to 1 before the damage initiated, and are updated due to damage accumulation of the associated damage modes.

Failure predicted by the criterion of f4 can be referred to as transverse matrix failure, while the matrix failure predicted by f5 , which is parallel to the layer, can be referred as the delamination mode when it occurs within the elements that are adjacent to the ply interface. Note that a scale factor S is introduced to provide better correlation of delamination area with experiments. The scale factor S can be determined by fitting the analytical prediction to experimental data for the delamination area.

FABRIC LAMINA DAMAGE FUNCTIONS

The fiber failure criteria of Hashin for a unidirectional layer are generalized to characterize the fiber damage in terms of strain components for a plain weave layer. The fill and warp fiber tensile/shear damage are given by the quadratic interaction between the associated axial and through the thickness shear strains, i.e.,

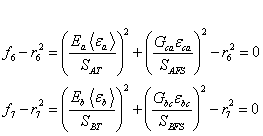(7)

where and are the axial tensile strengths in the fill and warp directions, respectively, and and are the layer shear strengths due to fiber shear failure in the fill and warp directions. These failure criteria are applicable when the associated or is positive. The damage thresholds r6 and r7 are equal to 1 without damage. It is assumed = S FS , and .

When or is compressive, it is assumed that the in-plane compressive damage in the fill and warp directions are given by the maximum strain criterion, i.e.,
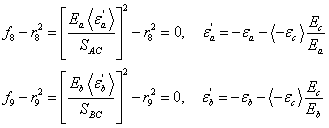(8)
where SAC and SBC are the axial compressive strengths in the fill and warp directions, respectively, and r8and r9 are the corresponding damage thresholds. Note that the effect of through the thickness compressive strain on the in-plane compressive damage is taken into account in the above two equations.

When a composite material is subjected to transverse impact by a projectile, high compressive stresses will generally occur in the impact area with high shear stresses in the surrounding area between the projectile and the target material. While the fiber shear punch damage due to the high shear stresses can be accounted for by equation (1), the crush damage due to the high through the thickness compressive pressure is modeled using the following criterion:

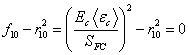(9)

where SFC is the fiber crush strengths and r10 is the associated damage threshold.

A plain weave layer can be damaged under in-plane shear stressing without occurrence of fiber breakage. This in-plane matrix damage mode is given by

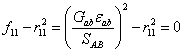(10)

where SAB is the layer shear strength due to matrix shear failure and r11 is the damage threshold .

Another failure mode, which is due to the quadratic interaction between the thickness strains, is expected to be mainly a matrix failure. This through the thickness matrix failure criterion is assumed to have the following form:

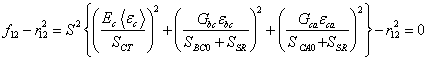(11)

where r12 is the damage threshold, is the through the thickness tensile strength, and and are the shear strengths for tensile ec . The damage surface due to equation (11) is parallel to the composite layering plane. Under compressive through the thickness strain, ec < 0, the damaged surface (delamination) is considered to be “closed”, and the damage strengths are assumed to depend on the compressive normal strain ec similar to the Coulomb-Mohr theory, i.e.,

(12)

where j is the Coulomb’s friction angle.

When damage predicted by this criterion occurs within elements that are adjacent to the ply interface, the failure plane is expected to be parallel to the layering planes, and, thus, can be referred to as the delamination mode. Note that a scale factor S is introduced to provide better correlation of delamination area with experiments. The scale factor S can be determined by fitting the analytical prediction to experimental data for the delamination area.

DAMAGE PROGRESSION CRITERIA

A set of damage variables vi with i = 1, …6, are introduced to relate the onset and growth of damage to stiffness losses in the material. The compliance matrix [S] is related to the damage variables as (Matzenmiller, et al., 1995) :

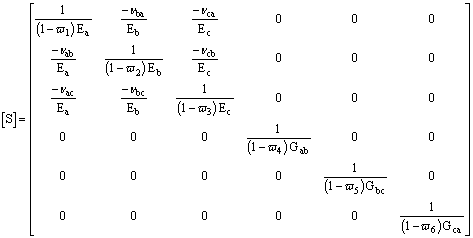(13)

The stiffness matrix C is obtained by inverting the compliance matrix, .

As suggested in Matzenmiller, et al., (1995) , the growth rate of damage variables, , is governed by the damage rule of the form

(14)

where the scalar functions control the amount of growth and the vector-valued functions q ij (i=1,…6, j=1,…12) provide the coupling between the individual damage variables (i) and the various damage modes (j). Note that there are five damage modes for the unidirectional model and seven damage modes for the fabric model.

The damage criteria fi – ri2 = 0 of equations (1 – 5) and (7 –13) provide the damage surfaces in strain space for the unidirectional and fabric models, respectively. Damage growth, > 0, will occur when the strain path crosses the updated damage surface fi – ri2 = 0 and the strain increment has a non-zero component in the direction of the normal to the damage surface, i.e., . Combined with a damage growth function , is assumed to have the form

(15)

Choosing

(16)

and noting that

(17)

for the quadratic functions of equations (1) to (5), lead to

(18)

where is the damage variable associated with the ith failure mode, and m is a material constant for softening behavior.

The damage coupling functions qij are considered for the unidirectional and fabric models as

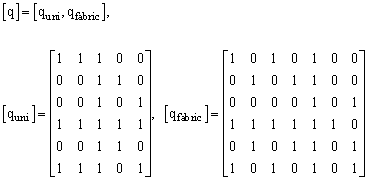(19)

Through equation (14), the above function qij relates the individual damage variables to the various damage modes provided by the damage functions of the unidirectional and fabric models.

For the unidirectional model, the damage coupling vectors qi1 and qi2 of equation (19) are chosen such that the fiber tensile/shear and compressive damage of modes 1 and 2 (equations A1 and A2, respectively) provide the reduction of elastic moduli E a , G ab , and G bc , due to , and , respectively. The coupling vector q i3 provides that all the elastic moduli are reduced due to the fiber crush damage of mode 3 (equation A3). For the transverse matrix damage mode 4 (equation A4), qi4 provides the reduction of Eb , Gab and Gbc , while the through the thickness matrix damage mode 5, qi5 provides the reduction of Ec , Gbc , and Gca .

For the fabric model, the damage coupling vector qi6 , qi7 , qi8 and qi9 are chosen for the fiber tensile/shear and compressive damage of modes 6 to 9 (equations A7 and A8) such that the fiber damage in either the fill or warp direction results in stiffness reduction in the loading direction and in the related shear directions. For the fiber crush damage of mode 10 of equation A9, the damage coupling vector qi10 is chosen such that all the stiffness values are reduced as an element is failed under the crush mode. For the in-plane matrix shear failure of mode 11 of equation (10), the stiffness reduction due to qi11 is limited to in-plane shear modulus, while the through the thickness matrix damage (delamination) of mode 12, the coupling vector qi12 is chosen for the through thickness tensile modulus and shear moduli.

Utilizing the damage coupling functions of equation (19) and the growth function of equation (18), a damage variable v i can be obtained from equation (14) for an individual failure mode j as

(20)

Note that the damage thresholds rj given in the damage criteria of equations (1 – 11) are continuously increasing functions with increasing damage. The damage thresholds have an initial value of one, which results in a zero value for the associated damage variable vi from equation (20). This provides an initial elastic region bounded by the damage functions in strain space. The nonlinear response is modeled by loading on the damage surfaces to cause damage growth with increasing damage thresholds and the values of damage variables vi . After damage initiated, the progressive damage model assumes linear elastic response within the part of strain space bounded by the updated damage thresholds. The elastic response is governed by the reduced stiffness matrix associated with the updated damage variables vi given in equation (13).

When fiber tensile/shear damage is predicted in a layer by equation (1) or (7), the load carrying capacity of that layer in the associated direction is reduced to zero according to damage variable equation (20). For compressive fiber damage due to equation (2) or (8), the layer is assumed to carry a residual axial load in the damaged direction. The damage variables of equation (20) for the compressive modes have been modified to account for the residual strengths of and in the fill and warp directions, respectively.

For through the thickness matrix (delamination) failure given by equation (5) or (11), the in-plane load carrying capacity within the element is assumed to be elastic (i.e., no in-plane damage). The load carrying behavior in the through the thickness direction is assumed to depend on the opening or closing of the matrix damage surface. For tensile mode, ec > 0, the through the thickness stress components are softened and reduced to zero due to the damage criteria described above. For compressive mode , ec < 0, the damage surface is considered to be closed, and thus, ec is assumed to be elastic, while ebc and eca are allowed to reduce to a sliding friction traction of equation (6) or (12). Accordingly, for the through the thickness matrix failure of mode 7 under compressive mode, the damage variable equation is further modified to account for the residual sliding strength SSR .

It is well known that it is difficult to obtain the softening response of most quasi-brittle materials including fiber-reinforced composites. The softening response heavily depends on the set-up and test machines, which can lead to very scattered results. Consequently the choice of damage parameters for each mode becomes an open issue. Generally, smaller values of ^m make the material more ductile whereas higher values give the material more brittle behavior. A methodology to systematically determine the model material properties for penetration modeling has been successfully established in [3].

The effect of strain-rate on the nonlinear stress-strain response of a composite layer is modeled by the strain-rate dependent functions for the elastic moduli and strength values , respectively, as
(21)

(22)

where C1 and C2 are the strain-rate constants. and are the modulus and strength values of and , respectively at the reference strain-rate .

ELEMENT EROSION

A failed element is eroded in any of three different ways:

• If fiber tensile failure in a unidirectional layer is predicted in the element and the axial tensile strain is greater than E_LIMIT. For a fabric layer, both in-plane directions are failed and exceed E_LIMIT.
• If compressive relative volume (ratio of current volume to initial volume) in a failed element is smaller than ECRSH.
• If expansive relative volume in a failed element is greater than EEXPN.

DAMAGE HISTORY PARAMETERS

Information about the damage history variables for the associated failure modes can be plotted in LSPOST. These additional variables are tabulated below:

<td “row”>Max (r1,r2)

History Variable			Description	Value	LS-POST Components
#	Uni	Fabric
1	Max (r6,r8)	Fiber mode in a	0 – elastic >1 – damage thresholds, Equations (1) to (11)	7
2	–	Max (r7,r9)		Fiber mode in b	8
3	r3	r10		Fiber crush mode	9
4	r4	r11		Perpendicular matrix mode	10
5	r5	r12		Parallel matrix / delamination mode	11
6			Element delamination indicator	0 – no delamination 1 – with delamination	12

 

REFERENCES

• Yen, C.F., (2002), “Ballistic Impact Modeling of Composite Materials,” Proceedings of 7 th International LS-DYNA Users Conference, May, 2002, Dearborn , Michigan , pp.6.15-6.26.
• Matzenmiller, A., Lubliner, J., and Taylor, R.L. (1995). “A Constitutive Model for Anisotropic Damage in Fiber-Composites,” Mechanics of Materials, 20, pp. 125-152.
• Xiao J.R., Gama, B.A. and Gillespie, J.W., (2005). Progressive damage and delamination in plain weave S-2 glass/SC-15 composites under quasi-static punch shear loading. ASME International Mechanical Engineering Congress. November 5-11, 2005 – Orlando , Florida .